จดหมายเหตุควอนตัมคอมพิวเตอร์

ผมต้องทำรายงานส่งอีกแล้วครับ คราวนี้เป็นหัวข้อ “สถาปัตยกรรมคอมพิวเตอร์ในอนาคต” ผมก็เลยคิดว่า ผมควรจะเอาเรื่องที่ผมเคยเขียนเมื่อหลาย ๆ ครั้งที่ผ่านมา จากหลาย ๆ ปีที่ผ่านมา อย่างเรื่องของ “ควอนตัมคอมพิวเตอร์” มาปะติดปะต่อเขียนใหม่ให้เป็นลักษณะของจดหมายเหตุ ที่มีการอ้างอิงวารสารวิชาการอย่างมีรูปแบบและเชื่อถือได้ ไม่ใช่การเล่าเรื่องเลื่อนลอยโดยไม่มีหลักฐานอ้างอิงอย่างครั้งที่ผ่าน ๆ มา อีกทั้งยังมีการใส่รายละเอียดเล่าถึงที่มาที่ไปอย่างครบถ้วน โดยพยายามใช้ภาษาอย่างง่ายที่สุด เพื่อให้คนที่ไม่ค่อยรู้ ได้รู้บ้างไม่มากก็น้อย

เอาเป็นว่าเริ่มเลยก็แล้วกันนะครับ …

บทนำ

ปัจจุบันโลกยังอยู่ในยุคของสถาปัตยกรรมดิจิทัลคอมพิวเตอร์ ซึ่งเป็นสถาปัตยกรรมที่พึ่งพาปรากฎการณ์ทางด้านอิเลกทรอนิกส์ในการขับเคลื่อน นั่นคือ ยังคงประมวลผลโดยพึ่งพาสัญญาณไฟฟ้ากระแสตรงแบบ 0 และ 1 ซึ่งทิศทางของสัญญาณไฟฟ้าเกิดจากการที่อิเล็กตรอนกระโดดออกจากอะตอมหนึ่งข้ามไปยังอีกอะตอมหนึ่งในทิศทางตรงข้ามกัน ในขณะเดียวกัน ปริมาณของทรานซิสเตอร์บนวงจรรวม ก็เพิ่มขึ้นเป็นเท่าตัวประมาณทุก ๆ สองปี ตามกฎของ Gordon E.  Moore

การที่ปริมาณของทรานซิสเตอร์บนวงจรรวมเพิ่มขึ้น ซึ่งทำให้การประมวลผลเร็วขึ้น ในขณะที่หน่วยประมวลผลยังคงมีขนาดเล็กเท่าเดิม แสดงให้เห็นว่า วงจรของหน่วยประมวลผลกำลังเล็กลงเรื่อย ๆ จนกระทั่งสุดท้าย วงจรของหน่วยประมวลผลก็จะมีขนาดเท่ากับอะตอมและไม่สามารถเล็กไปกว่านี้ได้ เพราะถ้าเล็กกว่าอะตอม ก็จะทำให้ปรากฎการณ์ทางไฟฟ้าที่เกิดจากการที่อิเล็กตรอนกระโดดออกจากอะตอมหนึ่งไปยังอีกอะตอมหนึ่งเกิดขึ้นไม่ได้ ซึ่งนั่นหมายความว่าจะไม่สามารถใช้ทฤษฎีแม่เหล็กไฟฟ้าเพื่อมาจัดการกับปรากฎการณ์นี้ได้

ด้วยปัญหาที่เกิดขึ้น ผนวกกับการที่ต่อไปวงจรจะมีขนาดเล็กลงจนอยู่ในระดับอะตอม (หรือเล็กกว่า) ซึ่งทำให้สามารถแสดงคุณสมบัติแบบควอนตัม (ก้อนพลังงานที่แกว่งตัว) ได้ และถ้าเป็นแบบนั้น แนวคิดของวงจรคอมพิวเตอร์ก็จะต้องเปลี่ยนไป จากเดิมที่ใช้ทฤษฎีแม่เหล็กไฟฟ้าเป็นพื้นฐานในการประดิษฐ์วงจร ก็ต้องเปลี่ยนเป็นการใช้ทฤษฎีกลศาสตร์ควอนตัมเป็นพื้นฐานในการประดิษฐ์วงจรแทน ทำให้ต้องมองว่าถ้าจะมีสิ่งใดมาแทนที่ดิจิทัลคอมพิวเตอร์ สิ่งนั้นก็คือควอนตัมคอมพิวเตอร์นั่นเอง

กลศาสตร์ควอนตัม

ฟิสิกส์ปัจจุบันประกอบด้วยวิชาหลักสองวิชา คือ ทฤษฎีสัมพัทธภาพ ซึ่งถูกคิดค้นโดย Albert Einstein และ ทฤษฎีฟิสิกส์ควอนตัม ซึ่งถูกคิดค้นโดยนักฟิสิกส์อัจฉริยะหลาย ๆ คน โดยทฤษฎีฟิสิกส์ควอนตัมก็แบ่งย่อยได้เป็น ทฤษฎีกลศาสตร์ควอนตัม ซึ่งใช้อธิบายความเป็นควอนตัมของสสาร และ ทฤษฎีควอนตัมสนาม ซึ่งใช้อธิบายอันตรกิริยาต่าง ๆ ในธรรมชาติ โดยคุณสมบัติสำคัญของทฤษฎีกลศาสตร์ควอนตัมที่น่าสนใจมีอยู่ 2 เรื่องใหญ่ ๆ ก็คือ 1)  เรื่องของหลักความไม่แน่นอนของ Werner Heisenberg คือ ถ้าเราสามารถวัดโมเมนตัมของอนุภาคได้อย่างแม่นยำ เราจะพบว่าเราไม่สามารถวัดตำแหน่งของอนุภาคได้อย่างแม่นยำ และ ถ้าเราสามารถวัดตำแหน่งของอนุภาคได้อย่างแม่นยำ เราจะพบว่าเราไม่สามารถวัดโมเมนตัมของอนุภาคได้อย่างแม่นยำ และ 2) เรื่องของความพัวพัน ซึ่งแสดงให้เห็นว่า ในระบบที่มีอนุภาค 2 อนุภาค ซึ่งอยู่ใกล้กันและมีอันตรกิริยากัน ในเวลาต่อมา ถ้าอนุภาคทั้ง 2 ถูกแยกออกจากกันไปไกลแสนไกลอย่างฉับพลันทันที ถ้ามีการวัดสมบัติของอนุภาคตัวแรก ข้อมูลที่ได้จะทำให้รู้ข้อมูลของอนุภาคตัวที่สองในทันทีทันใด โดยไม่จำเป็นต้องวัดคุณสมบัติของอนุภาคตัวที่สองเลย (สุทัศน์, 2556)

หลักความไม่แน่นอนของ Werner Heisenberg ในทฤษฎีกลศาสตร์ควอนตัมได้นำไปสู่การคิดค้นหลักการซ้อนทับในทางควอนตัมสำหรับคอมพิวเตอร์ หรือ Quantum Superposition ซึ่งเป็นผลให้แนวคิดเกี่ยวกับบิตในทางคอมพิวเตอร์เปลี่ยนไป จากเดิมที่เราคุ้นเคยกันว่า บิตในดิจิตอลคอมพิวเตอร์จะเป็นได้เพียงค่า 0 และ 1 ก็จะกลายเป็นว่าบิตในควอนตัมคอมพิวเตอร์จะมีค่า 0 หรือ 1 หรือเป็นได้ทั้ง 0 และ 1 ในเวลาเดียวกัน หรือที่เรียกว่า Superposition

แรกเริ่มนั้น Richard P.  Feynman ซึ่งเป็นนักฟิสิกส์ที่ได้รับรางวัลโนเบลในทฤษฎีควอนตัมสนาม ได้ตั้งข้อสังเกตว่า เราไม่สามารถจำลองปรากฎการณ์ของกลศาสตร์ควอนตัมที่แน่นอนอย่างมีประสิทธิภาพบนดิจิทัลคอมพิวเตอร์ได้ และคิดว่าการคำนวณโดยทั่วไปน่าจะมีประสิทธิภาพมากขึ้น หากใช้ปรากฎการณ์ควอนตัมเข้ามาช่วยในการคำนวณบนระบบควอนตัมจริง ๆ (R.  P.  Feynman, 1982)

การพิสูจน์สิ่งที่ Richard P. Feynman บอก หมายถึงการต้องสร้างควอนตัมคอมพิวเตอร์จริง ๆ ขึ้นมา เพื่อพิสูจน์ว่ามันสามารถคำนวณด้วยเวลาที่มีประสิทธิภาพมากขึ้น ซึ่งมันอาจไม่คุ้มหากสร้างขึ้นมาจริง ๆ แล้วกลับพบว่ามันไม่ได้คำนวณได้เร็วขึ้น ดังนั้น เพื่อลดต้นทุนในการพิสูจน์ จึงจำเป็นต้องพิสูจน์ทางอ้อมแทน ซึ่งวิธีการพิสูจน์ทางอ้อมที่เชื่อถือได้มากที่สุด คือ การพิสูจน์ด้วยสมการคณิตศาสตร์ และ Peter W.  Shor ก็ได้สร้างความประหลาดใจให้โลกได้เห็นว่า ด้วยขั้นตอนวิธีการแยกตัวประกอบเฉพาะและการหา Discrete Logarithm ที่คิดขึ้นสำหรับใช้บนควอนตัมคอมพิวเตอร์ จะสามารถประมวลผลได้ด้วยเวลาเป็น Polynomial เทียบกับการประมวลผลบนดิจิตอลคอมพิวเตอร์ ที่ต้องใช้เวลาเป็น Exponential (P.  W.  Shor, 1994) ซึ่งทำให้นักวิทยาศาสตร์เริ่มตระหนักว่าควอนตัมคอมพิวเตอร์ คือสิ่งที่คุ้มค่าหากคิดค้นมันขึ้นมาได้

ควอนตัมบิต

ในดิจิทัลคอมพิวเตอร์จะมองคุณสมบัติความเป็น “บิต” จากลูกคลื่นไฟฟ้า โดยหากคลื่นไฟฟ้ายกตัวในจังหวะนาฬิกาหนึ่ง จะถือว่าข้อมูลช่วงเวลาดังกล่าวเป็นบิต 1 ในขณะที่ถ้าคลื่นไฟฟ้าไม่ได้ยกตัวในจังหวะนาฬิกาหนึ่ง จะถือว่าข้อมูลช่วงเวลาดังกล่าวเป็นบิต 0 แต่สำหรับควอนตัมบิตจะเป็นอีกคุณสมบัติหนึ่ง

ควอนตัมบิตจะมองบิตในรูปของ Vector State บน Space และควอนตัมบิตจะไม่ได้มีค่าเพียง 0 หรือ 1 แต่อาจเป็นได้ทั้ง 0 และ 1 ในเวลาเดียวกัน หรือที่เรียกว่า Superposition ซึ่งการมีค่าเป็น 0 หรือ 1 คงไม่ต้องอธิบายเพิ่มเติม เพราะเหมือนกับดิจิทัลคอมพิวเตอร์อยู่แล้ว แต่สำหรับกรณี Superposition ที่เป็นได้ทั้ง 0 และ 1 ในเวลาเดียวกัน เป็นสิ่งที่ต้องอธิบายเพิ่มเติมเป็นพิเศษ และเพื่อให้เข้าใจแนวคิด Superposition นี้ จึงต้องใช้อนุภาคที่สามารถสังเกตได้โดยตรง คือ Photon เพื่อทดลองการจำกัดสนามไฟฟ้าของคลื่นแสงให้สั่นในระนาบเดียวกัน หรือ Photon Polarization ในการอธิบายคุณสมบัติของควอนตัมบิต (E.  Rieffel, W.  Polak, 2000)

ตัวอย่างในการทดลอง (E.  Rieffel, W.  Polak, 2000) คือ การใช้แสงความเข้มสูงยิงจากแหล่งกำเนิด ไปยังบริเวณเป้าหมาย โดยจะใช้แผ่นกรองแสง A ซึ่งจะกรองแสงในแนวนอน, แผ่นกรองแสง B ซึ่งจะกรองแสงในแนวนอนที่ 45 องศา และ แผ่นกรองแสง C ซึ่งจะกรองแสงในแนวตั้ง สำหรับกั้นแสงประกอบการทดลอง

เริ่มแรกจะใช้การยิงแสงความเข้มสูงซึ่งมีแนวคลื่นแสงแบบสุ่มให้กระทบเป้าหมาย โดยใช้แผ่นกรองแสง A ซึ่งจะกรองแสงในแนวนอน วางทับเพื่อบังคลื่นแสง ซึ่งจะทำให้ความเข้มของแสงลดลง 50%  (เป็นการสมมติจากความเป็นไปได้สูงสุด) และคลื่นแสงที่ออกมาจะเป็นแนวนอนทั้งหมด

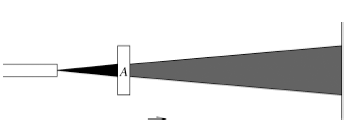
จากนั้นใช้แผ่นกรองแสง C ซึ่งจะกรองแสงในแนวตั้ง วางทับเพื่อบังคลื่นแสงแนวนอนที่ผ่านแผ่นกรองแสง A ซึ่งจะทำให้ความเข้มของแสงลดเหลือศูนย์ เมื่อตกกระทบเป้าหมาย เพราะคลื่นแสงแนวนอนไม่สามารถผ่านแผ่นกรองแสงสำหรับคลื่นแสงแนวตั้งได้

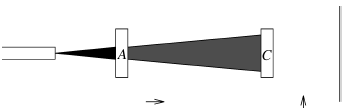
สุดท้าย ใช้แผ่นกรองแสง B ซึ่งจะกรองแสงในแนวนอน 45 องศา วางทับเพื่อบังคลื่นแสงระหว่างแผ่นกรองแสง A และแผ่นกรองแสง C ซึ่งจะทำให้ความเข้มแสงเล็กน้อยสามารถเล็ดลอดผ่านแผ่นกรองแสง C ตกกระทบยังเป้าหมายได้

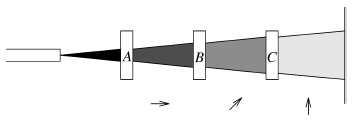
เพื่ออธิบายการทดลองนี้ จึงต้องมองทิศทางของแสงให้อยู่ในรูปของ Vector โดยให้มองว่าคลื่นแสงแนวตั้งเป็น Vector a และคลื่นแสงแนวนอนเป็น Vector b และให้มองว่า Vector a และ Vector b เป็นจำนวนเชิงซ้อน ดังนั้น การหาว่าทิศทางของคลื่นแสงสุดท้ายจริง ๆ เป็นค่าใด จะต้องอาศัยการตรวจวัดสภาวะของ Vector a และ Vector b ประกอบกัน โดยอาศัยหลักความน่าจะเป็นและทฤษฎีบทปีทากอรัสเข้ามาช่วยในการตรวจวัด ซึ่งเราจะเปรียบ Vector a โดยเขียนแทนด้วย  และเปรียบ Vector b โดยเขียนแทนด้วย  เพื่อตรวจสอบหา Vector ผลลัพธ์ ซึ่งสามารถเขียนแทนด้วย  และ 

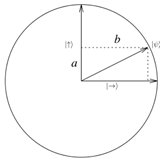
โดยการจะอธิบายให้เข้าใจในรายละเอียดได้นั้น จำเป็นที่จะต้องมีการนิยามสภาวะของ Vector State โดยใช้สัญลักษณ์ที่เรียกว่า Bra/Ket เข้ามาช่วย ได้แก่

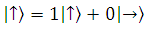1. หมายความว่า ทิศทางของคลื่นแสงผลลัพธ์ซึ่งเป็นแนวตั้งจะเกิดขึ้นได้ หากความน่าจะเป็นของคลื่นแสงแนวตั้งเป็น 100% และความน่าจะเป็นของคลื่นแสงแนวนอนเป็น 0% เปรียบได้กับการตรวจวัดหาควอนตัมบิตที่มีค่าเป็น 0
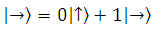2. หมายความว่า ทิศทางของคลื่นแสงผลลัพธ์ซึ่งเป็นแนวนอนจะเกิดขึ้นได้ หากความน่าจะเป็นของคลื่นแสงแนวตั้งเป็น 0% และความน่าจะเป็นของคลื่นแสงแนวนอนเป็น 100% เปรียบได้กับการตรวจวัดหาควอนตัมบิตที่มีค่าเป็น 1
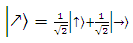3. หรือ 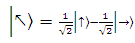หมายความว่า ทิศทางของคลื่นแสงผลลัพธ์จะเป็นได้ทั้งแนวตั้งและแนวนอน และเป็นได้ทั้งบวกและลบ ขึ้นอยู่กับความน่าจะเป็นของคลื่นแสงแนวตั้งและแนวนอนประกอบกัน (สมมติว่าความน่าจะเป็นของแนวตั้งและแนวนอนเกิดได้เท่ากัน) เปรียบได้กับการตรวจวัดหาควอนตัมบิตที่มีค่าเป็นได้ทั้ง 0 และ 1 ในเวลาเดียวกัน หรือที่เรียกว่า Superposition

จุดที่น่าสนใจอีกประการหนึ่งของควอนตัมบิตแบบ Superposition ก็คือ การที่มันจะเป็นได้ทั้ง 0 และ 1 ในเวลาเดียวกันเฉพาะก่อนการตรวจวัด แต่หากถูกตรวจวัดแล้วว่าเป็นค่าใด สภาวะควอนตัมบิตแบบ Superposition ก็จะยุติลง กลายเป็นควอนตัมบิตแบบธรรมดา (เป็น 0 หรือ 1) และสภาวะของอีกค่าหนึ่งก็จะถูกทำลายไปทันที

เพื่อให้เข้าใจอรรถประโยชน์ของควอนตัมบิตที่สามารถเป็นได้ทั้ง 0, 1 และ Superposition จะยกตัวอย่างควอนตัมบิตแบบ 2 บิตดังภาพด้านล่างนี้ โดยใช้ภาพวงกลมลูกศรชี้ขึ้นแทนควอนตัมบิต 1, ลูกศรชี้ลงแทนควอนตัมบิต 0 และลูกศรชี้เฉียงขึ้นขวา 45 องศาแทนควอนตัมบิตแบบ Superposition

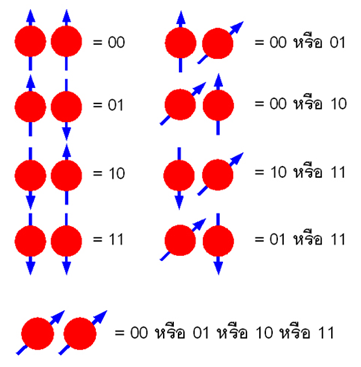
ซึ่งเมื่อดูจากรูปภาพที่ 5 แล้วจะเห็นว่า ด้วยควอนตัมบิตแบบ 2 บิต จะสามารถสร้างรูปแบบที่เป็นไปได้ถึง 9 รูปแบบ และจะสามารถสร้างผลลัพธ์ที่เป็นไปได้ถึง 16 กรณี

สำหรับการประยุกต์ทฤษฎีให้สามารถปฏิบัติได้นั้น นักวิทยาศาสตร์กำลังคัดเลือกสสาร, อะตอม, โมเลกุล หรือ แม้แต่อนุภาค ซึ่งมีคุณสมบัติเหมาะสม สามารถควบคุมสภาวะได้ มีความเสถียร และ สามารถสร้างวิธีการสังเกตตรวจวัดได้ ตามหลักการของควอนตัมบิต ซึ่งปัจจุบันก็มีเทคนิคหลาย ๆ อย่างถูกนำเสนอขึ้นมาไม่ว่าจะเป็นการใช้ ion traps, nuclear magnetic resonance, optical และ solid-state เป็นต้น

การเคลื่อนย้ายควอนตัม

ในทฤษฎีสัมพัทธภาพพิเศษของ Albert Einstein ได้พิสูจน์ให้โลกเห็นว่า ไม่มีสสารใดเคลื่อนที่เร็วไปกว่าความเร็วแสงได้ เพราะหากสสารใดเคลื่อนที่เร็วเท่ากับความเร็วแสง สสารดังกล่าวจะมีมวลเป็นอนันต์, ขนาดหดลงเป็นศูนย์ และ เวลาบนสสารดังกล่าวหยุดนิ่ง ซึ่งเป็นไปไม่ได้

แสงถือเป็นคลื่นแม่เหล็กไฟฟ้าชนิดหนึ่ง ในขณะที่ในธรรมชาติยังมีคลื่นแม่เหล็กไฟฟ้าชนิดอื่นอีก ไม่ว่าจะเป็น คลื่นวิทยุ, คลื่นไมโครเวฟ, รังสีอินฟราเรด, รังสีอัลตร้าไวโอเลต, รังสีเอ็กซ์, รังสีแกมม่า และ รังสีคอสมิก เป็นต้น ซึ่งคลื่นแม่เหล็กไฟฟ้าเหล่านี้ก็ล้วนเคลื่อนที่ด้วยความเร็วแสงทั้งนั้น และปัจจุบันมนุษย์เราก็ได้ใช้ประโยชน์จากคลื่นแม่เหล็กไฟฟ้าชนิดต่าง ๆ โดยเฉพาะการใช้คลื่นวิทยุเพื่อสื่อสารข้อมูลระหว่างกัน

การสื่อสารข้อมูลด้วยคลื่นวิทยุ ถือเป็นวิธีการสื่อสารที่เร็วที่สุดที่มนุษย์พึงกระทำได้ เพราะไม่ได้ขัดกับข้อเท็จจริงในทฤษฎีสัมพัทธภาพพิเศษ แต่ทว่า การค้นพบหลักความพัวพันทางควอนตัม ทำให้เกิดสิ่งที่ขัดแย้งกับความเป็นจริง คือ จะทำให้ระบบมีการสื่อสารกันได้อย่างทันทีทันใด หรือเรียกว่าการเคลื่อนย้ายควอนตัม ซึ่ง Einstein มองว่าเป็นสิ่งที่เป็นไปไม่ได้ เพราะถ้ามันทำได้จริงก็แสดงว่ามันเร็วกว่าแสง และมันจะละเมิดกฎของทฤษฎีสัมพัทธภาพพิเศษ ซึ่งภายหลังปัญหานี้ได้ถูกตั้งชื่อว่า EPR Paradox (A. Einstein, B. Podolsky, N. Rosen, 1935)

การค้นพบความพัวพันทางควอนตัม มีผลกระทบอย่างมากในเรื่องกรอบความคิดเกี่ยวกับระบบเครือข่ายและการสื่อสารข้อมูล เพราะมันสะท้อนให้เห็นว่าการสื่อสารข้อมูลในภายหน้า อาจไม่ต้องพึ่งพาระบบแบบมีสายหรือระบบไร้สาย เนื่องจากระบบสองระบบอาจสื่อสารกันเองได้อย่างทันทีทันใด แต่ทว่า ถึงแม้ว่าความพัวพันทางควอนตัมจะมีอยู่จริง ก็ไม่ได้หมายความว่าเราจะสามารถปฏิบัติให้เกิดขึ้นจริงได้โดยง่าย

ดังนั้น ในปัจจุบันนักวิทยาศาสตร์ยังคงไม่สามารถเคลื่อนย้ายควอนตัมได้โดยตรง หากแต่ใช้วิธีทางอ้อม โดยการใช้บิตปรกติในแบบดิจิทัลคอมพิวเตอร์ เพื่อนำส่งข้อมูลจากต้นทางสู่ปลายทาง โดยให้ต้นทางเข้ารหัสผลลัพธ์แบบควอนตัมบิตจำนวน 1 บิต ด้วยบิตปรกติจำนวน 2 บิต จากนั้นจึงส่งบิตปรกติจำนวน 2 บิตไปยังปลายทาง ผ่านเครือข่ายคอมพิวเตอร์ปรกติ เพื่อให้ปลายทางนำบิตปรกติ 2 บิตไปถอดรหัส เพื่อให้ได้ผลลัพธ์ของควอนตัมบิตจำนวน 1 บิตสำหรับนำไปใช้งานต่อไป (C. H. Bennett, at el., 1993)

ควอนตัมคอมพิวเตอร์

ปัจจุบัน การวิจัยทางด้านควอนตัมคอมพิวเตอร์ เป็นหัวข้อที่ได้รับความสนใจและมีการเติบโตมากขึ้นเรื่อย ๆ โดยได้มีการแบ่งกลุ่มงานวิจัยของควอนตัมคอมพิวเตอร์ออกเป็น 5 กลุ่มใหญ่ ๆ ได้แก่

1. ด้านทฤษฎีการประมวลผลแบบควอนตัม (Quantum Computing Theory)
2. ด้านภาษาโปรแกรมสำหรับควอนตัมคอมพิวเตอร์ (Quantum Programming)
3. ด้านสถาปัตยกรรมแบบควอนตัมคอมพิวเตอร์ (Quantum Computer Architecture)
4. ด้านสถาปัตยกรรมส่วนย่อยแบบควอนตัมคอมพิวเตอร์ (Quantum Computer Micro Architecture)
5. ด้านการควบคุมสภาวะของควอนตัมบิตให้อยู่ในลักษณะคงตัวและควบคุมได้ (Technology Building blocks)

โดยมีการจัดลำดับชั้นของกลุ่มงานวิจัยทางด้านควอนตัมคอมพิวเตอร์จากบนลงล่าง คือ จากลำดับของทฤษฎีที่จับต้องไม่ได้ สู่ลำดับของการปฏิบัติเป็นรูปธรรมที่จับต้องได้ ดังภาพด้านล่าง

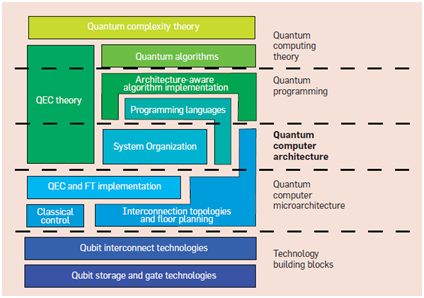
จุดสำคัญและถือว่าเป็นปัญหาใหญ่ของการสร้างควอนตัมคอมพิวเตอร์ก็คือ การควบคุมสภาวะของควอนตัมบิตให้มีความคงตัวและสามารถควบคุมได้ เนื่องจากสภาวะของควอนตัมบิตนั้นถูกรบกวนได้ง่ายจากสภาพแวดล้อมภายนอก และต้องไม่ลืมว่าควอนตัมบิตคือหัวใจสำคัญในการประมวลผล ดังนั้น การตรวจวัดสภาะวะของควอนตัมบิตได้อย่างแม่นยำจึงเป็นสิ่งที่สำคัญยิ่ง

จากภาพเราจึงเห็นว่าทุกกลุ่มงานวิจัยล้วนต่อยอดยึดโยงอยู่กับควอนตัมบิต เช่น การวิจัยเทคโนโลยีเพื่อจัดเก็บควอนตัมบิต, การวิจัยเพื่อให้สามารถตรวจวัดค่าจากควอนตัมบิตได้อย่างถูกต้อง, การวิจัยเพื่อเชื่อมต่อข้อมูลจากควอนตัมบิตออกสู่สภาพแวดล้อมภายนอก โดยไม่ทำให้ควอนตัมบิตเสียความคงตัว และการวิจัยเพื่อตีความควอนตัมบิตให้อยู่ในระบบเชิงตัวเลข เพื่อนำไปใช้ในระบบสมการต่อไป เป็นต้น

และนี่คือสาเหตุว่าทำไมควอนตัมคอมพิวเตอร์พาณิชย์เครื่องแรกของโลก ซึ่งผลิตโดยบริษัท D-Wave Systems จำกัด และมีขนาด 128 ควอนตัมบิต จึงมีขนาดใหญ่โตมาก อีกทั้งยังต้องอยู่ในพื้นที่เฉพาะที่มีขนาด 10 ตารางเมตร นั่นเพราะความจำเป็นที่ต้องสร้างชั้นการห่อหุ้มปกป้องเพื่อควบคุมอุณหภูมิ และรักษาสภาวะความคงตัวของควอนตัมบิตเอาไว้ให้ได้นั่นเอง

สำหรับภาษาโปรแกรมคอมพิวเตอร์ ซึ่งเป็นส่วนสำคัญอีกชิ้นหนึ่ง เพื่ออำนวยความสะดวก ให้มนุษย์สามารถสั่งงานควอนตัมคอมพิวเตอร์ได้นั้น ก็ได้มีความพยายามในการวิจัยเพื่อพัฒนาภาษาโปรแกรมคอมพิวเตอร์ใหม่ ๆ ขึ้นมา เพื่อให้มีไวยากรณ์สอดรับกับอัลกอริทึมแบบควอนตัม และให้มีควอนตัมบิตเป็นพื้นฐานของภาษา ไม่ว่าจะเป็นการสร้างภาษา Quipper (A. S. Green, et al, 2013) หรือภาษา QuaFL (A. Lapets, et al, 2013) เป็นต้น

การประยุกต์ใช้งาน

จากรายละเอียดที่กล่าวมาไม่ว่าจะเป็น กลศาสตร์ควอนตัม, ควอนตัมบิต, การเคลื่อนย้ายควอนตัม และ ควอนตัมคอมพิวเตอร์ ได้แสดงให้เห็นว่านักวิทยาศาสตร์คอมพิวเตอร์ จำเป็นที่จะต้องเปลี่ยนความคิดในหลาย ๆ อย่างเพื่อให้สอดรับกับสิ่งใหม่ ๆ ที่เกิดขึ้น ไม่ว่าจะเป็นความเข้าใจในทฤษฎีความซับซ้อนในการคำนวณเชิงควอนตัม และทฤษฎีการประมวลผลสารสนเทศเชิงควอนตัม (C. H. Bennett, P. W. Shor, 1998) รวมถึงการบุกเบิกประยุกต์ใช้ควอนตัมคอมพิวเตอร์เพื่อแก้ปัญหาในงานต่าง ๆ

โดยในช่วงเริ่มแรก นักวิทยาศาสตร์คอมพิวเตอร์ได้บุกเบิกที่จะนำควอนตัมคอมพิวเตอร์ไปใช้ในงานด้านความปลอดภัย เช่น การสร้างรหัสลับแบบควอนตัมเพื่อแลกเปลี่ยนกันระหว่างผู้รับและผู้ส่ง ก่อนที่จะมีการเข้ารหัสข้อมูลเพื่อรับส่งข้อมูลหากัน (D. Bruss, et al, 2007), การสร้างระบบเงินตราแบบควอนตัม เพื่อปกปิดประวัติการใช้จ่ายไม่ให้สามารถตรวจสอบได้ (S. Aaronson, et al, 2012) เป็นต้น

ปัจจุบัน การคิดค้นเพื่อประยุกต์ใช้งานควอนตัมคอมพิวเตอร์ยังคงอยู่ในวงจำกัด เนื่องจากควอนตัมคอมพิวเตอร์เชิงพาณิชย์ที่เริ่มออกสู่ตลาดนั้น ยังคงถูกใช้เพื่อการพิสูจน์ทฤษฎีทางด้านควอนตัมคอมพิวติ้งโดยหน่วยงานรัฐและบริษัทเอกชนชั้นนำของประเทศสหรัฐอเมริกา ดังนั้น คงต้องรอให้ควอนตัมคอมพิวเตอร์มีขนาดเล็กลง และราคาย่อมเยาว์จนผู้บริโภคทั่วไปสามารถเข้าถึงได้ และเมื่อนั้นการประยุกต์ใช้งานควอนตัมคอมพิวเตอร์ในด้านต่าง ๆ นอกจากงานด้านวิทยาศาสตร์และความมั่นคงก็จะมีตามมาเอง ซึ่งเมื่อถึงตอนนั้น เราก็จะได้เห็นนวัตกรรมใหม่ ๆ ที่ถูกต่อยอดโดยควอนตัมคอมพิวเตอร์ ออกมาโลดแล่นในตลาดผู้บริโภคอย่างแน่นอน

เอกสารอ้างอิง

A. Einstein, B. Podolsky, N. Rosen. “Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?” Physical Review, Vol. 47. (May 1935) : 777-780.

A. Lapets, et al. “QuaFL: A Typed DSL for Quantum Programming.” Proceedings of the 1st annual workshop on FPCDSL ’13. (September 2013) : 19-26.

A. S. Green, et al. “Quipper: A Scalable Quantum Programming Language.” Proceedings of the 34th ACM SIGPLAN conference on PLDI ’13. (June 2013) : 333-342.

C. H. Bennett, P. W. Shor. “Quantum Information Theory.” IEEE Transactions of Information Theory, Vol. 44, No. 6. (October 1998) : 2724-2742.

C. H. Bennett, et al. “Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels.” Physical Review Letters, Vol. 70, No. 13. (March 1993) : 1895-1899.

D. Bruss, et al. “Quantum Cryptography: A Survey.” ACM Computing Surveys, Vol. 39, No. 2, Article 6. (June 2007) : 1-27.

E. Rieffel, W. Polak. “An Introduction to Quantum Computing for Non-Physicists.” ACM Computing Surveys, Vol. 32, No. 3. (September 2000) : 300-335.

P. W. Shor. “Algorithms for Quantum Computation: Discrete Logarithms and Factoring.” IEEE. (1994) : 124-134.

P. W. Shor. “Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer.” Proceedings of the 35th Annual Symposium on Foundations of Computer Science. (November 1994) : 1-28.

R. P. Feynman. “Simulating Physics with Computers.” International Journal of Theoretical Physics, Vol. 21, No. 6/7. (1982) : 467-488.

R. V. Meter, C. Horsman. A Blueprint for Building a Quantum Computer. Communication of The ACM, Vol. 56, No. 10. (October 2013) : 94-93.

S. Aaronson, et al. Quantum Money. Communication of The ACM, Vol. 55, No. 8. (August 2012) : 84-92.

สุทัศน์ ยกส้าน. 113 ปี ฟิสิกส์ควอนตัม ที่ทำให้โลกเป็นอย่างทุกวันนี้. โลกวิทยาการ หนังสือพิมพ์ผู้จัดการออนไลน์. [Online]. (18 ตุลาคม 2556).

—-

ก็จบประมาณนี้แหล่ะครับ เอาเป็นว่า สำหรับใครที่สนใจเรื่องควอนตัมคอมพิวเตอร์ ผมขอแนะนำเลยนะครับว่า ให้ทำความเข้าใจสมการจำนวนเชิงซ้อนที่ใช้แทนค่าควอนตัมบิตเพื่อหา Superposition อ่ะครับ พอเข้าใจแล้ว แก้สมการได้แล้ว ก็จะต่อยอดทางควอนตัมคอมพิวเตอร์ได้ในภายภาคหน้าครับ สู้ ๆ ครับ