ผมเพิ่งได้มีโอกาสอ่าน แผน
หมวดหมู่: Quantum Computer
โม้เกี่ยวกับเทคโนโลยี Quantum Computer

คิดว่าทุกคนคงทราบกันแล้วว
บล็อกนี้เอาสั้น ๆ นะ สืบเ
ตอนนี้ Deep Learning เป็น
พวกเราคงจำข่าวที่ Google
เข้าใจว่าตอนนี้หลาย ๆ คนใ
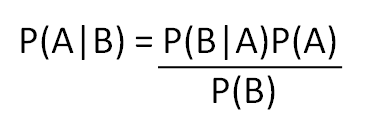
ทฤษฎีบทของเบย์เป็นทฤษฎีคว
การหยั่งรู้ล่วงหน้าแบ่งได
ผมต้องทำรายงานส่งอีกแล้วค
การเคลื่อนย้ายมวลสาร ก็คื
